Określanie ustawień sieciowych danego komputera i jego lokalizacji w sieci
Ustawienia sieciowe komputera w sieci Obecnie najczęściej wykorzystywane są sieci oparte o rodzinę protokołów TCP/IP. Protokół IP (Internet Protocol) realizuje warstwę sieciową, a protokoły TCP (Transport Control Protocol) i UDP (User Datagrams Protocol) realizuja warstwę transportu. W powszechnym użyciu są dwie wersje protokołu IP: wersja 4 (IPv4) wersja 6 (IPv6) Podstawową różnicą pomiędzy tymi protokołami sprowadza...
Terminologia sieciowa i warstwowy model sieci
Sieć komputerowa. Sieć komputerową tworzą co najmniej dwa komputery połączone w taki sposób, że mogą wymieniać między sobą dane, takie jak pliki, komunikaty tekstowe czy poczta elektroniczna lub korzystać ze wspólnych zasobów i usług sieciowych. Dzięki sieciom można m. in. współdzielić urządzenia, zasoby dyskowe, wydruki, dostęp do Internetu oraz różnych mechanizmów zabezpieczeń i organizacji sieci. Wymagane jest jednak spełnienie...
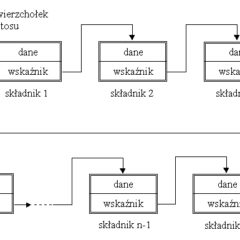
Wskaźniki i tworzenie zmiennych dynamicznych
Rodzaje zmiennych W języku Pascal zmienne dzielą się na statyczne i dynamiczne. Zmienna statyczna tworzona jest w trakcie kompilacji programu i istnieje do momentu jego zakończenia lub też do momentu zakończenia funkcji lub procedury, w której została zadeklarowana. Program w momencie uruchamiania otrzymuje od systemu operacyjnego fragment pamięci o rozmiarze 64KB przeznaczony na dane statyczne – fragment ten nazywamy segmentem...
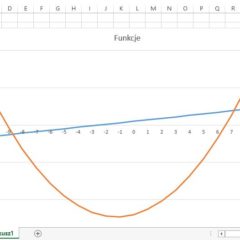
Wybrane funkcje arkusza kalkulacyjnego
Arkusz kalkulacyjny pozwala na bezpośrednie zapisywanie na ekranie monitora wzorów, wg których wykonywane są obliczenia na bieżąco wyświetlając na tym samym ekranie wyniki otrzymane dla konkretnych danych metodą wpisaną w arkusz. Zmiana wartości jednej z danych powoduje automatyczne przeliczenia wszystkich zależnych od niej wielkości. Pliki arkusza to zeszyty podzielone na pojedyncze arkusze. Zbudowane są z komórek, których kolumny...
Obliczenia w arkuszu kalkulacyjnym. Formatowanie tabeli arkusza i prezentacja danych na wykresach
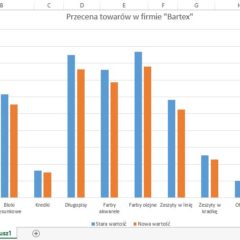
Zadanie 1 Dokonaj przeceny towarów hurtowni wg wzoru poniżej: Wartości wyświetlone na czerwono zostały obliczone za pomocą odpowiednich formuł. Dane przedstaw na wykresie